整数的存储

整数在计算机中的表示分为有符号数和无符号数。
有符号数：可以区分正负的数
无符号数：无正负的类型（只有正值）

就像 C 语言中的整型数分为 int、unsigned int …其中的 unsigned 就是无符号类型的数，它只能表示正数。

无符号数的表示

计算机使用固定的位数来存储数据，比如计算机使用8位来存储一种类型的数，那么即使这个数并不需要使用8位二进制来表示，计算机依旧会用固定的8位来存储，方式就是在前面补 0。

例如：25 —> 0001 1001

如果在一个数太大，位数不够怎么办？舍去高位，在计算中出现这种情况叫做溢出，也许很多人都见到过正数相加结果位负数的情况。

正如这种情况下，最高位 1 会被直接舍弃，最后结果是 1。

这也说明了对于一种类型的数，它是有范围限制的，比如 C 语言中的占 32 位的 unsigned int 的表示范围为：[0, 4294967295]

那负数该怎么表示呢？

有符号数的表示

就有人想出了可以拿出一位用来做符号位，对于8位正数而言：0xxxxxxx 对于8位负数而言：1xxxxxxx，这就是所谓的原码表示。

这样表示是可以，但是对于设计运算的电路来说不是很容易，因为我们无法使用加法来替代减法。

这个结果是明显不对的，我们总不能还给减法再设计一个电路吧。

聪明的人们就想出了对于负数换一种表示，对于负数来说将它们对应的正数的每一位二进制位都取反来表示这个负数。

例如对于 -2 来说，将 0000 0010 取反变成 1111 1101，这样的表示，叫反码。

结果还是不对啊，但好像仔细观察发现好像结果仅仅和正确答案相差 1，如果我们给负数的表示再加上1呢？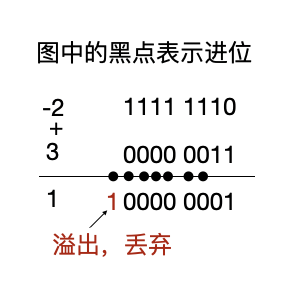

对于这样先取反再加 1 的表示，叫做补码。

总结：

  1. 计算机使用固定的位来存储数据
  2. 对于有符号数来说，计算机使用补码来存储

实数的存储

我们在编程的时候，是可以使用小数计算的，毕竟我们日常生活中使用的都是实数，那么计算机是怎么存储小数的？

小数在计算机中可以有两种方法表示，一种是定点表示；另一种是浮点表示。

一般来说，定点格式可表示的数值的范围有限，但要求的处理硬件比较简单。而浮点格式可表示的数值的范围很大，但要求的处理硬件比较复杂。采用定点数表示法的计算机称为定点计算机，采用浮点数表示法的计算机称为浮点计算机。

定点数

所谓定点格式，即约定机器中所有数据的小数点位置是固定不变的（毕竟硬件无法真的表示小数点），定点数分为定点小数和定点整数。

定点小数

定点小数的纯小数，约定的小数点位置在符号位之后、有效数值部分最高位之前。

该定点小数为：0.1011011 这是二进制的小数表示，转化为十进制为：
1∗2−1+0∗2−2+1∗2−3+1∗2−4+0∗2−5+1∗2−6+1∗2−71*2^{-1}+0*2^{-2}+1*2^{-3}+1*2^{-4}+0*2^{-5}+1*2^{-6}+1*2^{-7}

定点整数

定点整数是纯整数，约定的小数点位置在有效数值部分最低位之后。

和有符号的表示类似，该定点整数为 01011011 转换的方式和原码一样

浮点数

采用浮点表示的数叫浮点数，之所以叫浮点数，是因为和定点数想比，小数点的位置是浮动的。其实很简单，它的表示方法和科学计数法类似：

N=JE∗FN=J^E*F （F 是尾数，E 是指数）

严格来说，J 的值可以是任何值，但是现在的计算机都遵循 IEEE 754 浮点标准，所以 J 的值我们就取 2。

既然是在计算机中，那么每一个数的表示所用的位数是固定的，所以浮点表示的设计者需要在尾数和指数之间进行取舍，因为尾数的的位数大小影响的是数值的精度，而指数的的位数大小影响的是数值表示的范围。

我们先来介绍一个概念：规格化

规格化

对于一个采用科学计数法表示的数，如果没有前导的零并且小数点左边只有一位整数，则可称这个数是规格化（normalized）数

是不是看完感觉这是啥？没关系举个🌰就明白了：

对于1.0∗10−91.0*10^{-9} 这个数来说，1.0∗10−91.0*10^{-9} 就是一个规格化的科学技术，而0.1∗10−80.1*10^{-8}​ 和1.0∗10−101.0*10^{-10} 这样的表示就不是规格化数。

规格化有什么用？

  • 简化了浮点数的数据交换
  • 简化了浮点算术运算
  • 提高了存储的数字的精度

浮点数的一般表示

浮点数在计算中是如何存储的？

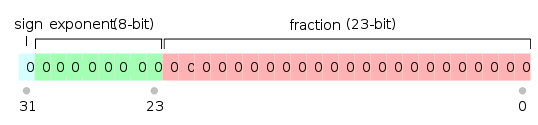
单精度浮点数的表示

从图中可以看出，对于32位的浮点数来说，1位指示符号，8位表示指数，23位表示尾数

所以浮点数的值：(−1)S∗F∗2E(-1)^S*F*2^E

虽然浮点数可以表示很大和很小的数，但是毕竟计算机能够表示的数是离散的是有限个，而数学中的数是无限的。

上溢：正的指数太大而导致指数域无法表示

下溢：负的指数太大而导致指数域无法表示

简单来说就是超出了浮点数的表示范围（毕竟指数决定了浮点数的范围）

IEEE 754 标准

对于浮点数的表示，为了能够表示更高的精度，IEEE 754 标准隐藏了规格化二进制浮点数的前导数 1，也就是说尾数部分的数全是规格化数表示中的小数点后的部分。

例如尾数：110101001010 表示的是 1.110101001010，在这种设计下增加了一位有效位，提高了精度。

对于指数部分：为了简化分类，指数部分没有采用补码的方式表示，而是使用了叫做 带偏阶的计数法。

例如指数的位数为k，指数的无符号表示为 e，则E=e−(2k−1−1)E=e-(2^{k-1}-1)，2k−1−12^{k-1}-1 为偏置。

IEEEE 754 将数分为三类：

  • 规格化的数
  • 非规格化的数
  • 特殊值

拿单精度和双精度数来举例：

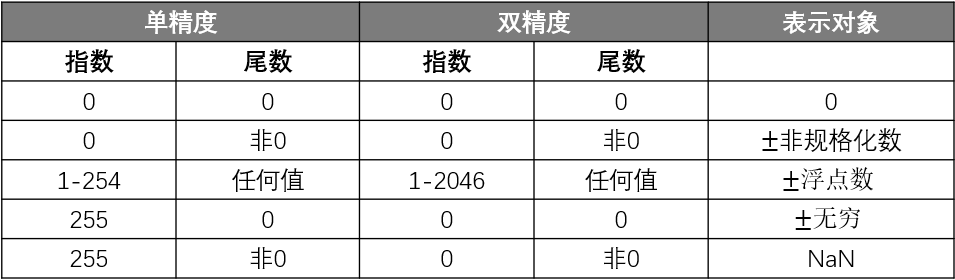
注意：非规格数，计算的时候不需要加上1，因为 IEEE 754是对规格的二进制数隐藏了前导的 0

JavaScript 的 number 类型就是使用的 IEEE 754 标准的双精度浮点数，所以 js 的数字类型才会有 Infinity，NaN

整数的乘法运算

我们先讨论无符号数的乘法运算。我们先回忆一下我们如何做十进制的乘法：

这两个数都是十进制数，但是由于他们都只含有1和0，即使把他们当作二进制也没有不对的地方。我们来看这个乘法是如何实现的，第一位源操作数叫被乘数，第二个源操作数叫乘数。因为二进制数的某一位只可能是1或0，所以每一位乘出来的数要么是被乘数，要么是0。
如果乘数这次拿出的是1，我们就需要将被乘数放到某个合适的位置，如果是0，我们需要将0放到合适的位置。

对于二进制我们怎么处理呢？对于8位整数的乘法，乘出来的结果最大是16位，所以我们需要用16位来表示乘积，我们不妨用一个16位的寄存器保存被乘数和乘积（乘积默认位0），用一个8位的寄存器来保存乘数，那么乘法的过程应该就是这样：

  1. 我们检测乘数的最后一位是1还是0
  2. 如果乘数的末尾是1，那么乘积 + 被乘数
  3. 乘数右移一位
  4. 被乘数左移一位
  5. 再重复步骤一，直到该过程已经执行了8次

对于32位，64位的整数的乘法也是一样的道理，那要是有符号数呢？那也很简单，将他们都转为正数并记住符号位，然后用同样的方式进行运算，但是需要少执行一次（符号位不需要参加），然后如果符号是相异的就转为负数的形式。

综上所述：我们通过加法和移位运算就可以是实现二进制数的乘法运算。

整数的除法

未完待续。。。