堆
在队列中,调度程序反复提取队列中第一个作业并运行,因为实际情况中某些时间较短的任务将等待很长时间才能结束,或者某些不短小,但具有重要性的作业,同样应当具有优先权。堆即为解决此类问题设计的一种数据结构。
堆可以实现优先队列(priority queue),有地方发也被称为优先队列,尽管名为优先队列,但堆并不是队列。
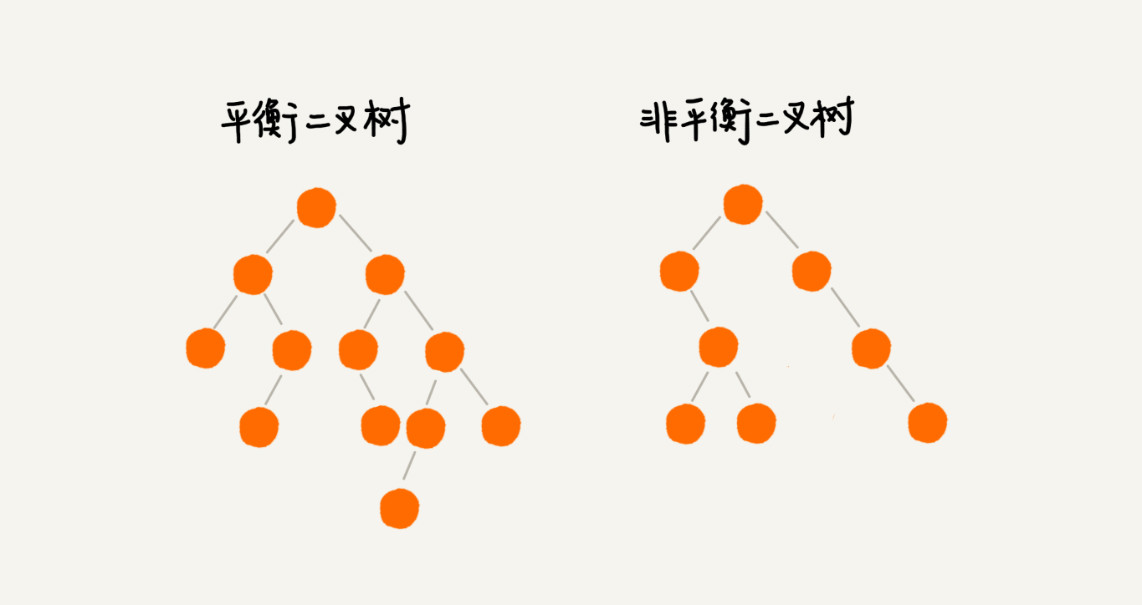
堆也是一种树状的数据结构,常见的堆实现:
基本接口
1
2
3
4
5
6
7
8
9
| interface Heap<T> {
size: number;
isEmpty(): boolean;
clear(): void;
add(ele: T): void;
peek(): T | null;
removeTop(): T | null;
replace(ele: T): T | null
}
|
二叉堆
堆的一个经典的实现是完全二叉树,这样实现的堆成为二叉堆。由于是完全二叉树,可以利用数组来作为底层实现的数据结构。
和二叉树类似,任意一个节点的子堆也是一个二叉堆,二叉堆的子节点不区分大小。
最大堆: 任意节点的值总是大于子节点的值,任意节点的子节点也是一个最大堆
最小堆: 任意节点的值总是小于子节点的值,任意节点的子节点也是一个最小堆
使用数组来实现完全二叉树,索引的规律就需要捋清楚。在不将数组第一位作为哨兵的情况下,对于任意一个索引 i :
- 父节点索引为
Math.floor((i - 1) / 2) - 左子节点的索引
2 * i + 1 - 右子节点索引
2 * i + 2
定义二叉堆的数据结构
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| abstract class BinaryHeap<T> implements Heap<T> {
protected heap: T[] = [];
protected abstract compare(i: number, j: number): boolean;
private swap(i: number, j: number): void {
const len = this.size;
if (i < 0 || j < 0 || i >= len || j >= len) {
throw new RangeError('index is outof range')
}
const heap = this.heap;
[heap[i], heap[j]] = [heap[j], heap[i]];
}
}
|
对于二叉堆来说,新添加的元素都是添加在末尾,删除一定是删除的头部元素。
但是经过添加删除之后,堆中元素的优先级就会发生改变不符合二叉堆的性质就需要进行调整。
siftUp
新添加的元素在末尾,就会导致该元素所在的子堆不满足要求,需要和自己的父元素比较查看是否需要调整,所谓调整就是和父节点交换位置,调整完之后需要重复直到不需要调整或者调整到堆的根节点。
这个步骤称之为 siftUp:
1
2
3
4
5
6
| private siftUp(k: number) {
while (k > 0 && this.compare(k, (k - 1) >> 1)) {
this.swap((k - 1) >> 1, k);
k = (k - 1) >> 1;
}
}
|
siftDown
删除的都是头部元素,为了效率一般都是将末尾元素和头部交换再删除末尾元素。接着堆可能会不满足条件,就需要从根开始调整,这个步骤是和 siftUp 相反的过程。和子元素比较来判断是否需要交换,一直重复直到满足条件或者到底了。
1
2
3
4
5
6
7
8
9
10
| private siftDown(k: number) {
const N = this.size;
let j;
while ((j = (k << 1) + 1) < N) {
if (j < N - 1 && this.compare(j + 1, j)) { j++; }
if (!this.compare(j, k)) { return; }
this.swap(k, j);
k = j;
}
}
|
添加和删除
添加和删除之后就需要调整堆中数据的位置。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| public add(ele: T): void {
this.heap.push(ele);
this.siftUp(this.size - 1);
}
public removeTop(): T | null {
const N = this.size;
if (N === 0) {
return null;
} else if (N === 1) {
return <T>this.heap.pop();
}
const top = this.heap[0];
this.heap[0] = <T>this.heap.pop();
this.siftDown(0);
return top;
}
|
替换
1
2
3
4
5
6
7
8
9
10
| public replace(ele: T): T | null {
const N = this.size;
if (N === 0) {
return null;
}
const old = this.heap[0];
this.heap[0] = ele;
this.siftDown(0);
return old;
}
|
建堆
关于堆的另一个操作就是,在线性的时间内建一个堆。一般用于堆排序。
1
2
3
4
5
6
7
| protected heapify(data: T[]) {
this.heap = data;
const start = (this.size >> 1) - 1;
for (let i = start; i >= 0; i--) {
this.siftDown(i);
}
}
|
TopK问题
从N个整数中,找出最大的前K个数(K远远小于N)。
使用排序的做法,需要 O(nlgn) 的时间复杂度,而使用二叉堆来做只需要 O(nlgk) 的复杂度。
做法:
- 建一个空的最小堆
- 遍历N个数据
- 前 K 个数据直接加入堆
- K + 1个数据开始,如果大于堆顶元素就
replace
- 最后堆中剩余的数据就是最大的前 K 个数据
1
2
3
4
5
6
7
8
9
10
| function topK(data: number[], k: number) {
const heap = new MinHeap<number>();
data.forEach((num, i) => {
if (i < k) {
heap.add(num);
} else if (num > (heap.peek() as number)) {
heap.replace(num);
}
})
}
|