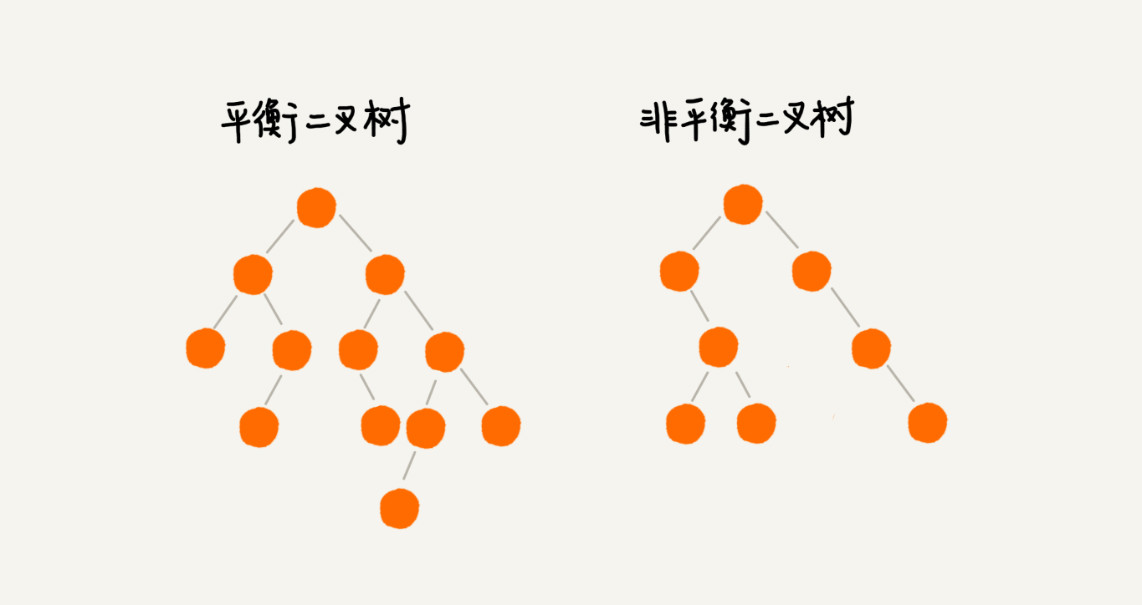
二叉树
节点的定义
1
2
3
4
5
6
7
8
9
10
11
12
13
| class TreeNode<T> {
public val: T;
public right: TreeNode<T> | null = null;
public left: TreeNode<T> | null = null;
public parent: TreeNode<T> | null = null;
constructor(val: T) {
this.val = val;
}
isLeave() {
return this.left === null && this.right === null;
}
}
|
遍历
对于二叉树来说,比较重要的一个操作就是遍历。遍历分为前序、中序、后序、层序遍历,也称为深度优先搜索和广度优先搜索。
深度优先搜索中包含了前序、中序、后序遍历。
深度优先
对于深度优先搜索最先想到的应该就是递归实现,这也是最简单的实现方式。
1
2
3
4
5
6
7
8
9
| function traversal(root: TreeNode<T> | null): void {
if (root) {
traversal(root.left);
tranersal(root.right);
}
}
|

虚线就是深度优先搜索时的路径,可以发现度为0节点会被访问一次,度为1的节点会被访问2次,度为2的节点会被访问3次。
所谓的前序、中序、后序遍历指的是第几次碰到该节点的时候执行访问,也就是常说的先访问自己再访问左子树和右子树、先访问左子树再访问自己然后访问右子树、先访问左子树和右子树再访问自己。
迭代实现
基本上所有的递归都可以改为迭代,递归的特点就是保留了以前的状态,所以我们也就需要一个栈来帮助我们保存以前访问过的节点。
前序遍历
一种实现方式:
root 入栈- 循环以下操作直到栈空:
- pop 出
top 然后访问 top.right 入栈top.left 入栈
1
2
3
4
5
6
7
8
9
10
| function preorderTraversal(root: TreeNode<T>): void {
const stack: TreeNode<T>[] = [];
stack.push(root);
while (stack.length) {
const node = stack.pop();
node.right && stack.push(node.right);
node.left && stack.push(node.left);
}
}
|
中序遍历
这种方式将访问的代码换到上面的循环中也就变成了前序遍历,个人觉得这种方式更加的容易想到和理解。
1
2
3
4
5
6
7
8
9
10
11
12
13
| function inorderTraversal( root: TreeNode<T>): void {
const stack: TreeNode<T>[] = [];
let node: TreeNode<T> | null = root;
while (node || stack.length) {
while (node) {
stack.push(node);
node = node.left;
}
node = stack.pop();
node = node.right;
}
}
|
后序遍历
后序遍历的非递归是比较难想的,这里提供一种思路:

我们按照虚线的路线入栈,就是根节点先入栈,然后依次循环的分别让右子节点,左子节点入栈。
如果对于这样的二叉树到最后的节点依次出栈就是后序遍历的顺序,但是这是所有的右子树只有根节点的情况,所以在循环中需要判断以下每一次是循环是需要继续入栈还是出栈访问。
循环中的判断条件应该是:栈顶节点是叶子节点 / 上一次访问的节点是栈顶节点的子节点(右子树不止存在根节点的情况)。
整体步骤就是:
root 入栈- 循环以下操作直到栈空:
- 如果栈顶节点是叶子节点 / 上一次访问的节点是栈顶节点的子节点
- 否则
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| function postorderTraversal(root: TreeNode<T>): void {
const stack: TreeNode<T>[] = [];
stack.push(root);
let prev: TreeNode<T> | null = null
while (stack.length) {
const top = stack[stack.length - 1];
if (top.isLeave() || (top.left === prev || top.right === prev)) {
prev = stack.pop()
} else {
top.right && stack.push(top.right);
top.left && stack.push(top.left);
}
}
}
|
广度优先
所谓的 BFS 就是利用队列将同一层的节点保存起来然后访问,在访问的同时将下一层的节点也入队列。
1
2
3
4
5
6
7
8
9
10
| function levelOrderTraversal(root: TreeNode<T>) {
const queue: TreeNode<T> = [];
queue.push(root);
while (queue.length) {
const node = queue.shift();
node.left && queue.push(node.left);
node.right && queue.push(node.right);
}
}
|
前驱节点
所谓前驱节点就是一个节点在中序遍历时的前一个节点。
对于二叉搜索树来说很好找就是左子树的最大值,但是对于一般的二叉树就稍微麻烦点。
- 对于一个存在左子树的节点来说,中序遍历的前一个节点就是它左子树的最
right 的节点,例如图中8、4、13等节点。 - 对于一个不存在左子树的节点来说
- 如果有父节点的存在并且能一直向上找到向左的开叉,则就存在前驱节点,例如:6、10、11
- 否则就没有前驱节点,例如:1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| function predecessor(root: TreeNode<T>): TreeNode<T> | null {
if (root.left) {
let node = root.left;
while (node.right) {
node = node.right;
}
return node;
}
while (root.parent && root === root.parent.left) {
root = root.parent;
}
return root.parent;
}
|
后继节点
后继节点类似于前驱节点,它是一个节点在中序遍历时的后一个节点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| function successor(root: TreeNode<T>): TreeNode<T> | null {
if (root.right) {
let node = root.right;
while (node.left) {
node = node.left;
}
return node;
}
while (root.parent && root === root.parent.right) {
root = root.parent;
}
return root.parent;
}
|
二叉搜索树
二叉查找树的定义:
- 若任意节点的左子树不空,则左子树上所有节点的值均小于它的根节点的值
- 若任意节点的右子树不空,则右子树上所有节点的值均大于它的根节点的值
- 任意节点的左、右子树也分别为二叉查找树
对于二叉搜索树比较重要的操作是添加和删除。
这里采用了递归的实现,其实完全可以使用迭代来实现,尤其是当我们的节点中定义了 parent 属性,使用迭代实现更加方便。
添加
添加操作比较简单,大于的往右子树添加,小于的往左子树添加。
1
2
3
4
5
6
7
8
9
10
11
12
13
|
function add(root: TreeNode<T> | null, val: T): TreeNode<T> {
if (root === null) {
root = new TreeNode(val);
} else if (compare(val, root.val) < 0) {
root.left = add(root.left, val);
root.left.parent = root;
} else if (compare(val, root.val) > 0) {
root.right = add(root.right, val);
root.right.parent = root;
}
return root;
}
|
删除
相比于添加,删除稍微复杂一些。需要分度为0、1、2三种情况。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
function delete(root: TreeNode<T> | null, val: T): TreeNode<T> | null {
if (root) {
if (compare(val, root.val) < 0) {
root.left = delete(root.left, val);
} else if (compare(val, root.val) > 0) {
root.right = delete(root.right, val);
} else {
if (root.isLeave()) {
root = null;
} else if (root.right && root.left) {
root.val = (<TreeNode<T>>successor(root)).val;
root.right = delete(root.right, root.val);
} else {
if (root.left) {
root.left.parent = root.parent;
root = root.left;
}
if (root.right) {
root.right.parent = root.parent;
root = root.right;
}
}
}
}
return root;
}
|
tip: 本文只涉及核心逻辑,具体的代码实现可以参考GitHub项目。