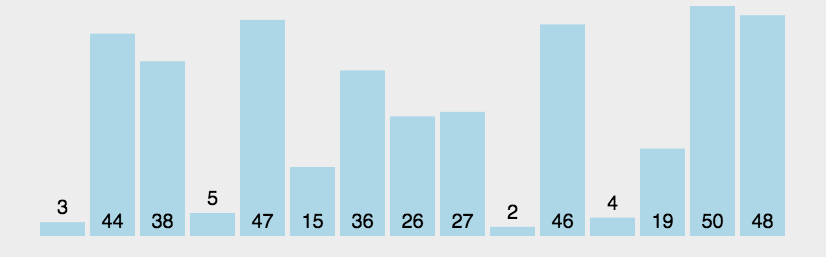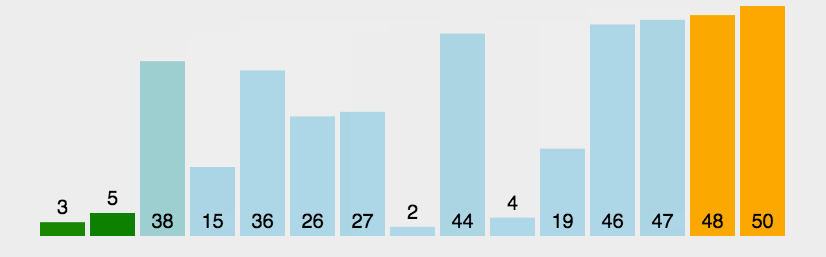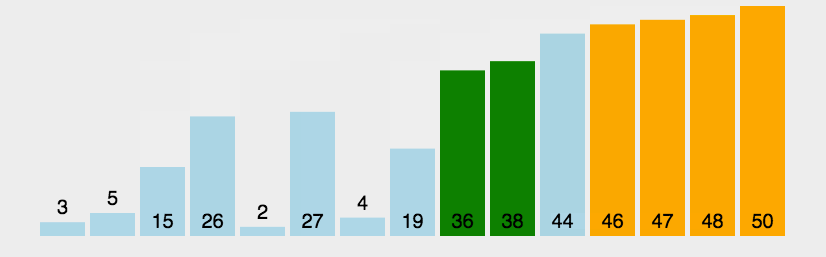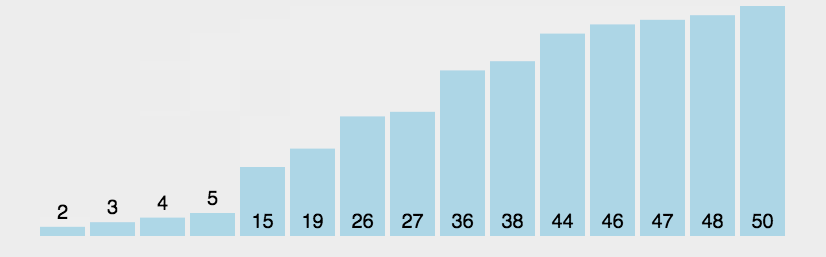冒泡排序
冒泡排序重复地走访过要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。
这个算法的名字由来是因为越小/大的元素会经由交换慢慢“浮”到数列的顶端。
冒泡排序的思路
- 从头开始比较每一对相邻元素,如果不符合升序/降序的要求,就交换它们的位置
- 经历过几轮比较,第几大/小的元素一定在倒数第几个
- 忽略已经找到的元素,重复执行比较交换,直到全部元素有序
图示
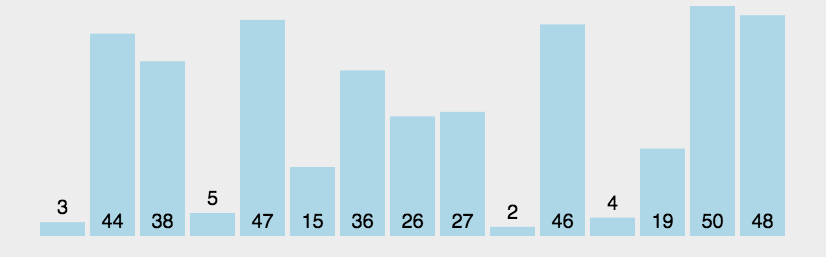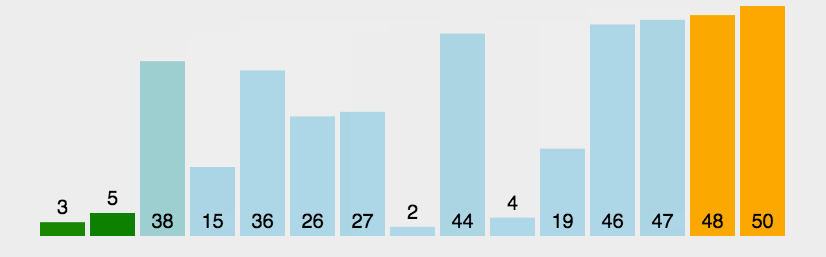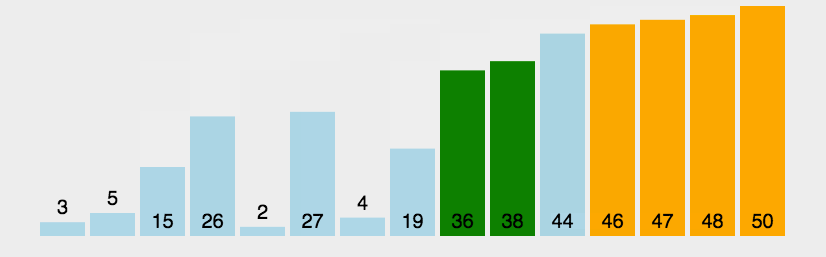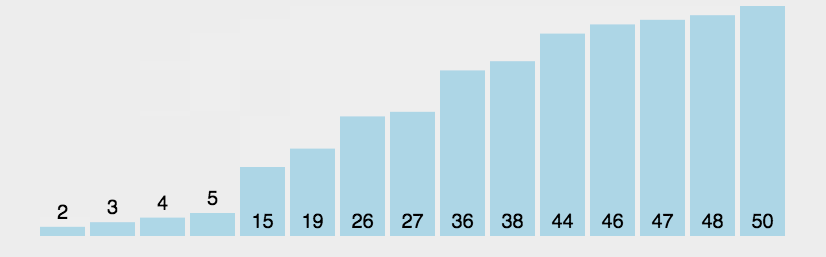
实现
1
2
3
4
5
6
7
8
9
10
| function bubbleSort<T>(arr: T[], comparator: Comparator = defaultComparator) {
const len = arr.length;
for (let i = 0; i < len - 1; i++) {
for (let j = 0; j < len - 1 - i; j++) {
if (comparator(arr[j], arr[j + 1]) > 0) {
[arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
}
}
}
}
|
优化1
如果在一轮比较中没有数据交换,意味着整个数组已经有序,可以直接结束排序。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| function bubbleSort<T>(arr: T[], comparator: Comparator = defaultComparator) {
const len = arr.length;
let sorted;
for (let i = 0; i < len - 1; i++) {
sorted = true;
for (let j = 0; j < len - 1 - i; j++) {
if (comparator(arr[j], arr[j + 1]) > 0) {
[arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
sorted = false;
}
}
if (sorted) {
break;
}
}
}
|
优化2
在排序过程中数组分为两个区域:一个是末尾的有序区,一个是前面的无序区。
真正的有序区不是已经找到的元素组成,而是由最后一次执行交换的下标到数组末尾。
每次比较仅比较到有序区,以及判断每一次是否有序可以减少比较次数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| function bubbleSort<T>(arr: T[], comparator: Comparator = defaultComparator) {
const len = arr.length;
let lastExchangeIndex = 0,
sortedBorder = len - 1;
for (let i = 0; i < len - 1; i++) {
lastExchangeIndex = 0;
for (let j = 0; j < sortedBorder; j++) {
if (comparator(arr[j], arr[j + 1]) > 0) {
[arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
lastExchangeIndex = j;
}
}
if (lastExchangeIndex === 0) {
break;
}
sortedBorder = lastExchangeIndex;
}
}
|
选择排序
选择排序是一种简单直观的排序算法。它的工作原理:首先在未排序序列中找到最小/大元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小/大元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
选择排序思路
- 从序列中找出最大/小的元素,和起始位置的元素进行交换
- 和冒泡排序一样,每一轮都可以决定一个数据的位置
- 忽略已经找到的元素,重复执行直到全部有序
图示
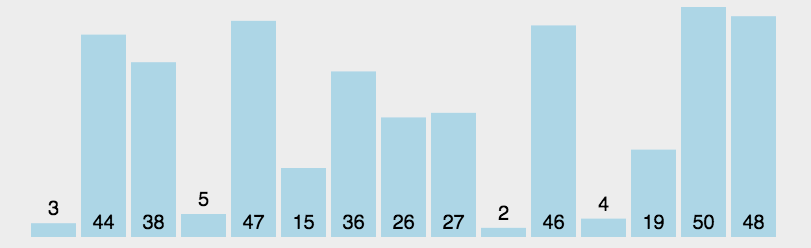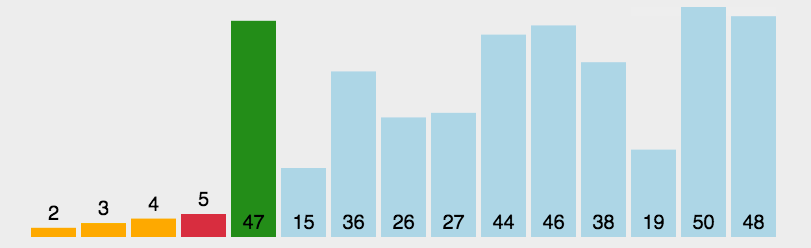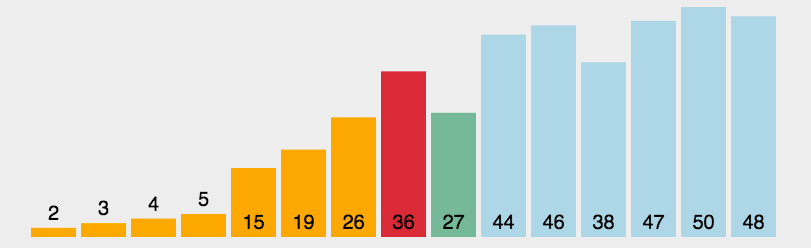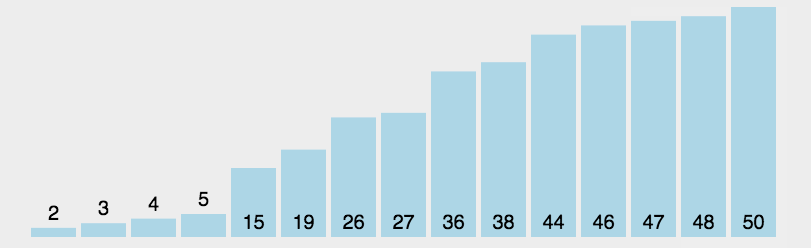
实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| function selectionSort<T>(arr: T[], comparator: Comparator = defaultComparator) {
const len = arr.length;
let minIndex;
for (let i = 0; i < len; i++) {
minIndex = i;
for (let j = i + 1; j < len; j++) {
if (comparator(arr[minIndex], arr[j]) > 0) {
minIndex = j;
}
}
if (minIndex !== i) {
[arr[i], arr[minIndex]] = [arr[minIndex], arr[i]];
}
}
}
|
插入排序
插入排序的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
插入排序思路
- 插入排序将序列分为2个部分
- 头部是已经排好序的
- 尾部是待排序的
- 从头开始扫描每一个元素,并将其放入头部合适的位置,使头部数据保持有序,类似于扑克牌
图示
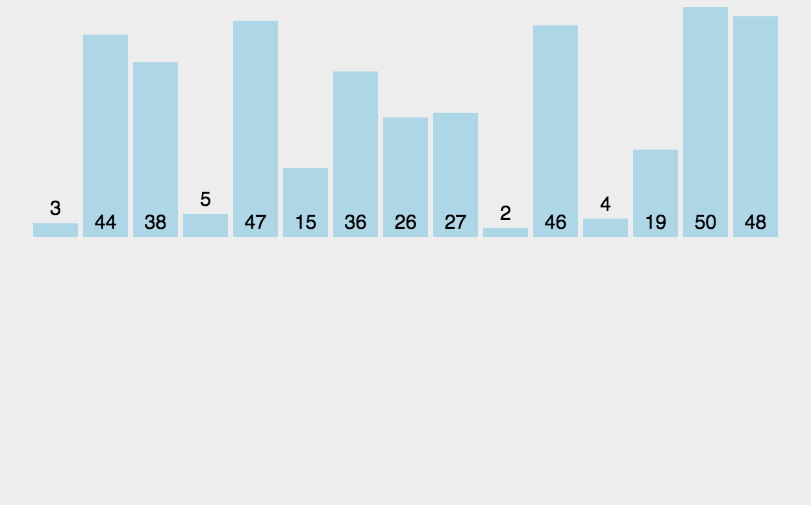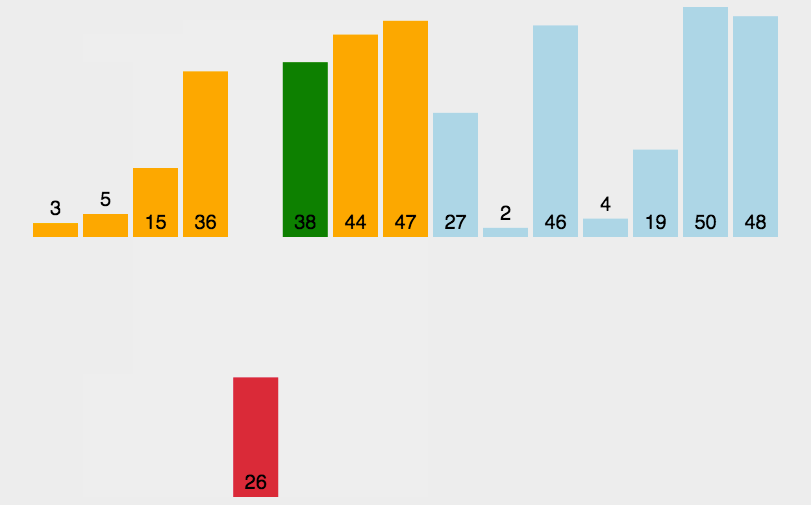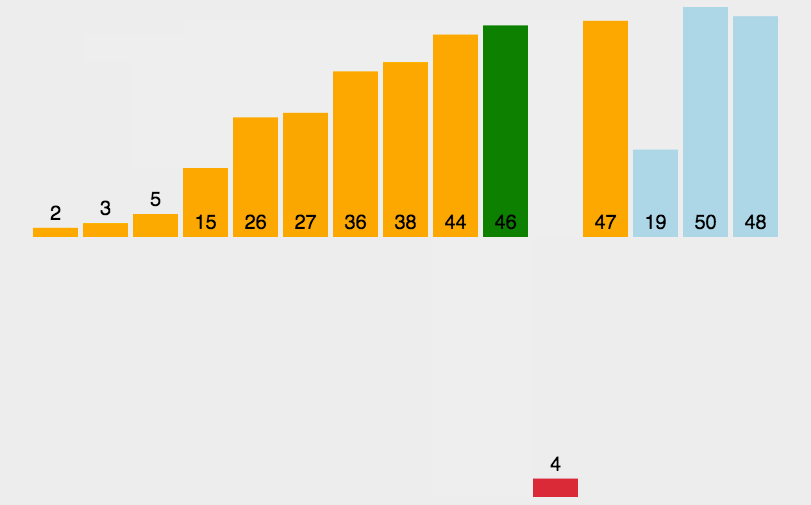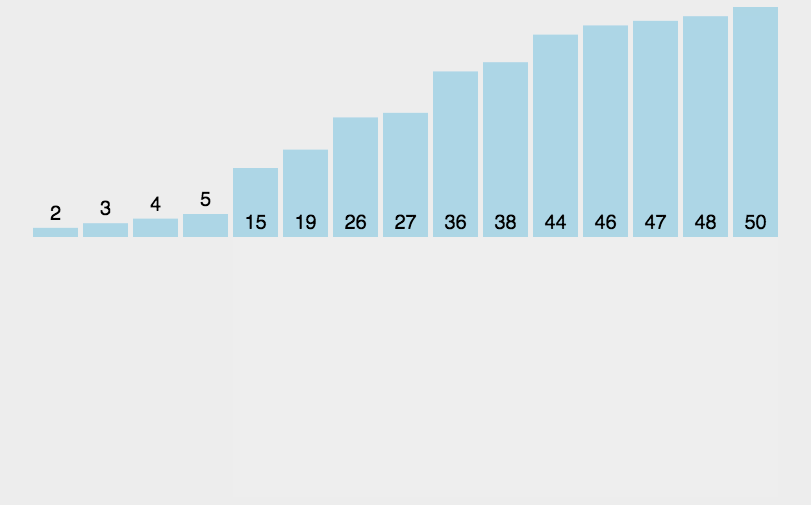
实现
1
2
3
4
5
6
7
8
| function insertionSort<T>(arr: T[], comparator: Comparator = defaultComparator) {
const len = arr.length;
for (let i = 1; i < len; i++) {
for (let j = i; j > 0 && comparator(arr[j], arr[j - 1]) < 0; j--) {
[arr[j], arr[j - 1]] = [arr[j - 1], arr[j]];
}
}
}
|
优化
将新数据插入过程的交换换为挪动,能减少交换次数提高效率,也更加符合扑克牌中的插入。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| function insertionSort<T>(arr: T[], comparator: Comparator = defaultComparator) {
const len = arr.length;
let curValue: T,
curIndex: number;
for (let i = 1; i < len; i++) {
curValue = arr[i];
curIndex = i;
for (let j = i; j > 0 && comparator(arr[j], arr[j - 1]) < 0; j--) {
[arr[j], arr[j - 1]] = [arr[j - 1], arr[j]];
curIndex = j - 1;
}
arr[curIndex] = curValue;
}
}
|
性能
插入排序的性能取决于输入元素的初始顺序,数组越接近有序排序越快。
将数据的交换变为挪动,可以大幅提高插入排序的速度,这样可以减少一半访问数组的次数。
时间复杂度:
- 最坏 O(n2)
- 最好 O(n)
- 平均 O(n2)
希尔排序
对于大规模乱序数组插入排序很慢,因为插入排序只会交换相邻的元素,元素只能一点一点地从数组的一端移动到另一端。
希尔排序基于插入排序,简单的改进了一下,交换不相邻的元素以对数组的局部进行排序,最终将局部有序的数组排序。
希尔排序的思想是使数组中任意间隔为h的元素都是有序的,这样的数组称为 h有序数组。
在进行排序时,h很大就能很容易的移动元素,也为实现更小的h创造便利,直到 h为1,数组就能够排序。
递增序列: h所取的值组成的序列,例如:h 从 N 通过 h/3 变为1。
实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| function shellSort<T>(arr: T[], comparator: Comparator = defaultComparator) {
const len = arr.length;
let h = 1;
while (h < Math.floor(len / 3)) {
h = h * 3 + 1;
}
while (h >= 1) {
for (let i = h; i < len; i++) {
for (let j = i; j >= h && comparator(arr[j], arr[j - h]) < 0; j -= h) {
[arr[j], arr[j - h]] = [arr[j - h], arr[j]];
}
}
h = Math.floor(h / 3);
}
}
|
性能
希尔排序比插入排序要快的多,并且数组越大,优势越大。
希尔排序更高效的原因是它权衡了子数组的规模和有序性。排序开始时子数组短,排序之后子数组部分有序,这两种情况都适合插入排序。
子数组部分有序的程度取决于递增序列的选择,递增序列的选择是一个数学问题。
时间复杂度:使用$ 1/2(3^k - 1)$序列达不到平方级别,在最坏的情况下比较次数和N3/2成正比
归并排序
归并排序是采用分治法的一个非常典型的应用。先让每个子序列有序,将已有序的子序列合并,得到完全有序的序列。
归并排序思路
- 将当前序列平均分为2个子序列
- 将2个子序列排序
- 将排序完成的2个子序列合并为一个有序序列
实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| function mergeSort<T>(arr: T[], comparator: Comparator = defaultComparator) {
const aux = new Array<T>(arr.length);
const sort = (lo: number, hi: number) => {
if (hi <= lo) { return; }
const mid = lo + Math.floor((hi - lo) / 2);
sort(lo, mid);
sort(mid + 1, hi);
merge(lo, mid, hi);
}
const merge = (lo: number, mid: number, hi: number) => {
let i = lo, j = mid + 1;
for (let k = lo; k <= hi; k++) {
aux[k] = arr[k];
}
for (let k = lo; k <= hi; k++) {
if (i > mid) {
arr[k] = aux[j++];
} else if (j > hi) {
arr[k] = aux[i++];
} else if (comparator(aux[j], aux[i]) < 0) {
arr[k] = aux[j++];
} else {
arr[k] = aux[i++];
}
}
}
sort(0, arr.length - 1);
}
|
性能
归并排序是一种渐进最优的基于比较排序的算法。
时间复杂度:由于总是平均分割,最好、最坏、平均时间复杂度都是 O(nlgn)
空间复杂度:递归 + 辅助数组 O(lgn + n) —> O(n)
快速排序
快速排序是一种分治的排序算法,类似于归并排序。
在实现上的区别就是:前一种递归调用发生在处理数组之前,后一种递归调用发生在处理数组之后。
快速排序的思想:
不同于归并排序将数组等分,快排则是从数列中挑出一个元素(称为 pivot )将数组切分为两部分,一部分是小于该基准的元素,另一部分是大于该基准的元素。切分之后,pivot 就位于这两部分元素的中间。
以选择数组第一个元素为基准为例,进行切分:

递归地在另外两部分进行切分,则当所有切分完毕之后,子数组有序了,整个数组也有序了。
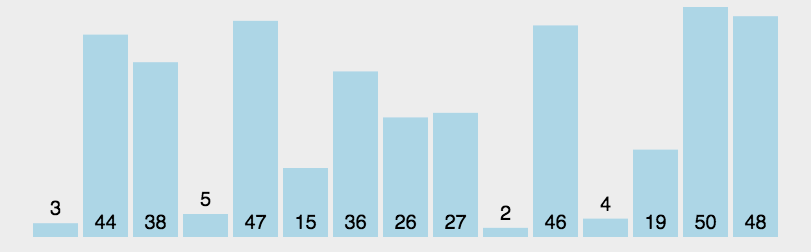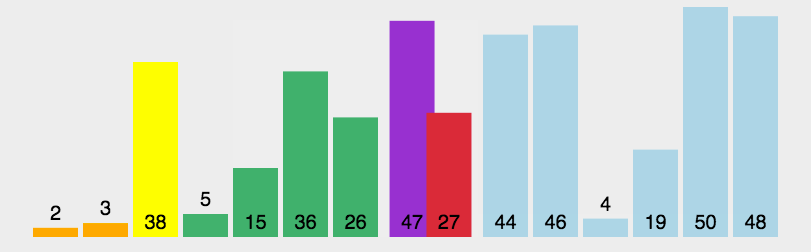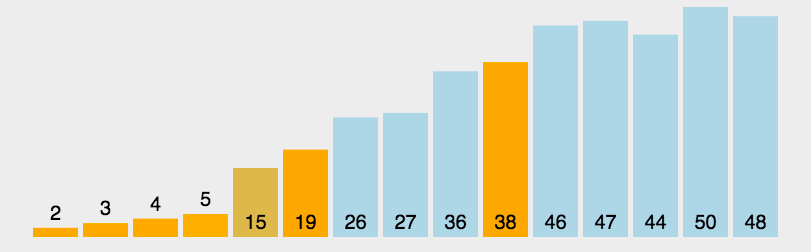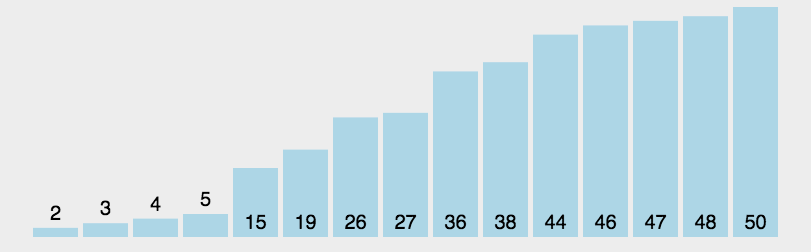
实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| function quickSort<T>(arr: T[], comparator: Comparator = defaultComparator) {
const sort = (lo: number, hi: number) => {
if (hi <= lo) { return; }
const pivot = partition(lo, hi);
sort( lo, pivot - 1,);
sort( pivot + 1, hi,);
}
const partition = (lo: number, hi: number) => {
let i = lo, j = hi + 1;
const v = arr[lo];
while (true) {
while (comparator(arr[++i], v) < 0) if (i == hi) break;
while (comparator(v, arr[--j]) < 0) if (j == lo) break;
if (i >= j) break;
[arr[i], arr[j]] = [arr[j], arr[i]];
}
[arr[lo], arr[j]] = [arr[j], arr[lo]];
return j;
}
sort(arr, 0, arr.length - 1);
}
|
性能
快速排序由冒泡排序演变而来,由于使用了分治法,所以原本需要比较N轮,只要比较 logN 轮。
快速排序的效率依赖于数组切分的效果,也就是取决于pivot的值。
最好的切分效果是每次都对半切分,最差的情况每次选中的都是最小/大的元素,每次只会确定一个元素位置,退化成冒泡排序。
时间复杂度:
- 最好:O(nlgn)
- 最坏:O(n2)
- 平均:O(nlgn)
空间复杂度:O(lgn)
快速排序对于数据随机的大数组效率很高,保持随机性的两种方式:
- 排序前打乱数组
- 在
partition 随机选择一个 pivot
对于小数组,快速排序比插入排序慢,一般的做法是在排序小数组时使用插入排序。
将 sort 方法进行改进:
1
2
3
4
5
6
7
8
| const sort = (lo: number, hi: number) => {
if (hi <= lo + M) {
insertionSort(arr, comparator);
}
const pivot = partition(lo, hi);
sort( lo, pivot - 1,);
sort( pivot + 1, hi,);
}
|
堆排序
堆排序指的是利用堆这种数据结构来辅助完成数组的排序。
堆排序的思路非常简单,首先在线性的时间内建一个堆,接着利用堆删除元素的思路进行排序。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| function heapSort<T>(arr: T[], comparator: Comparator<T> = defaultComparator) {
MaxHeap.buildHeap(arr);
for (let i = arr.length - 1; i > 0; i--) {
[arr[i], arr[0]] = [arr[0], arr[i]];
siftDown(arr, 0, i, comparator);
}
}
function siftDown<T>(arr: T[], k: number, N = arr.length, comparator: Comparator<T> = defaultComparator) {
let j;
while ((j = (k << 1) + 1) < N) {
if (j < N - 1 && comparator(arr[j + 1], arr[j]) > 0) {
j++;
}
if (!(comparator(arr[j], arr[k]) > 0)) {
return;
}
[arr[k], arr[j]] = [arr[j], arr[k]];
k = j;
}
}
|